Media and simulators
A complete list can be found here.
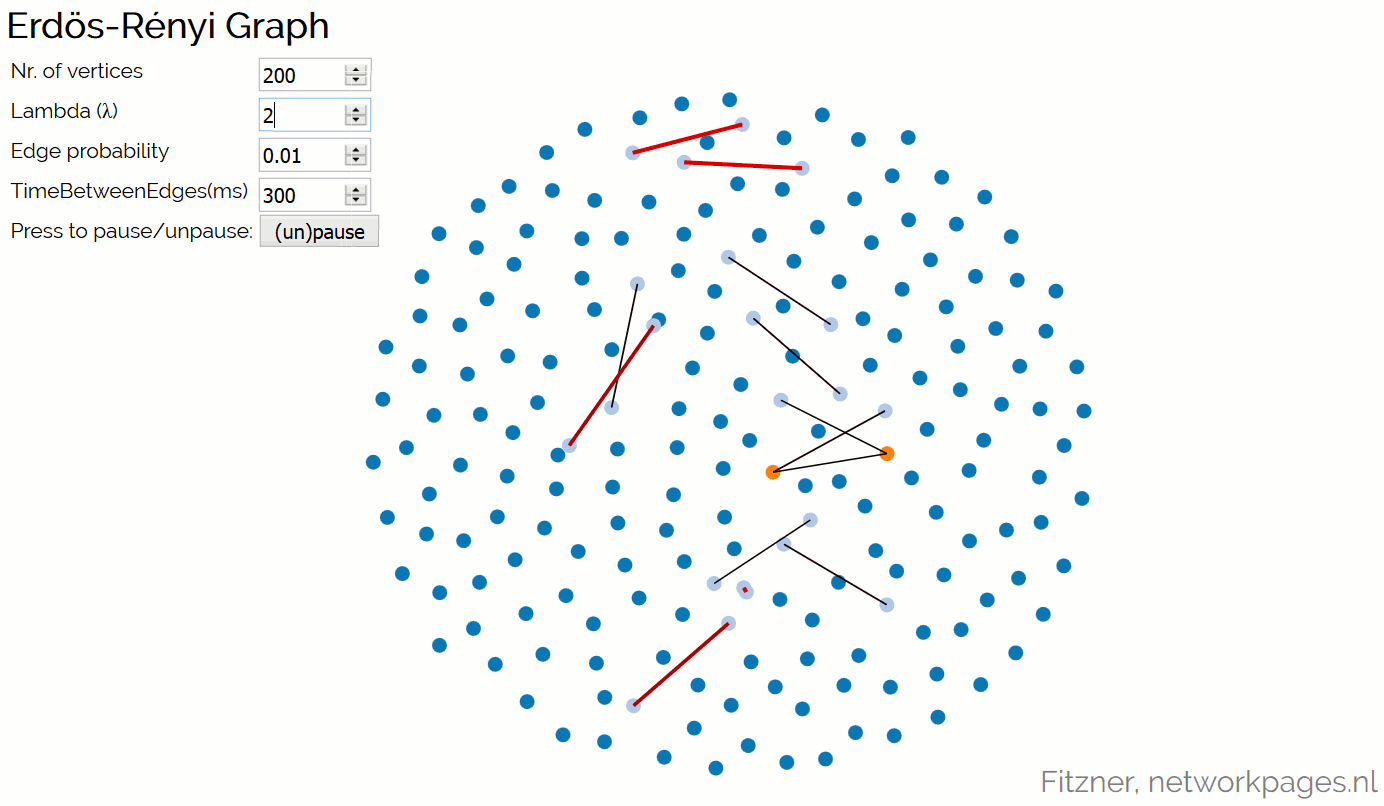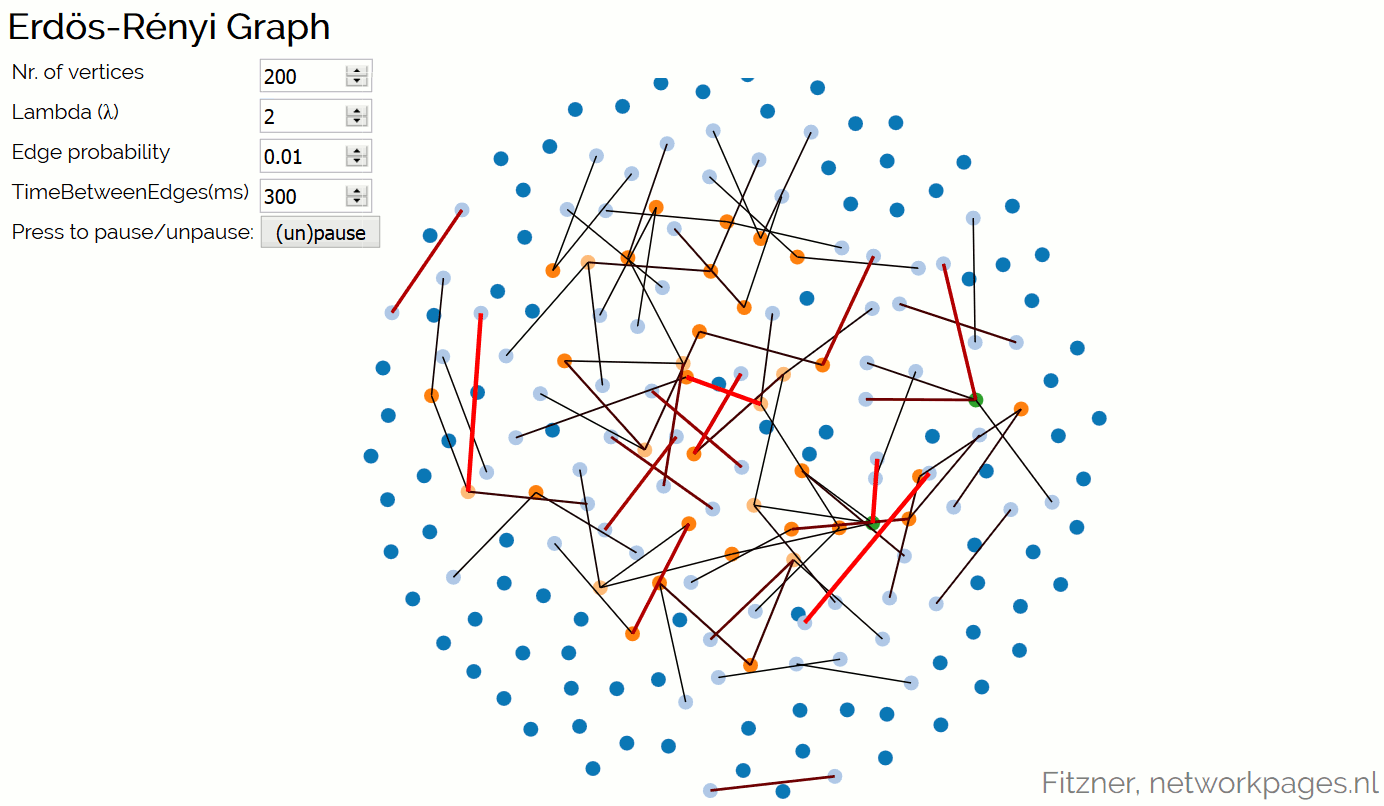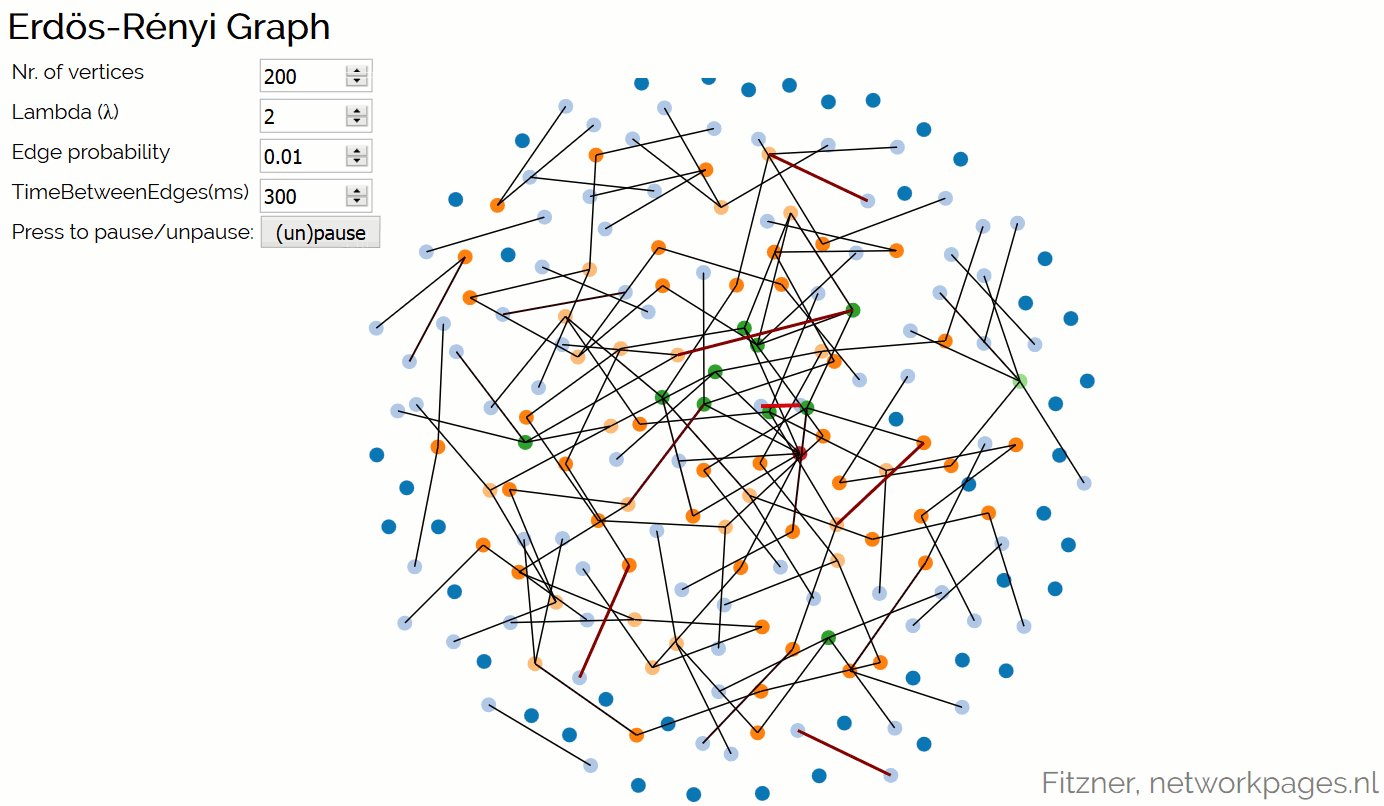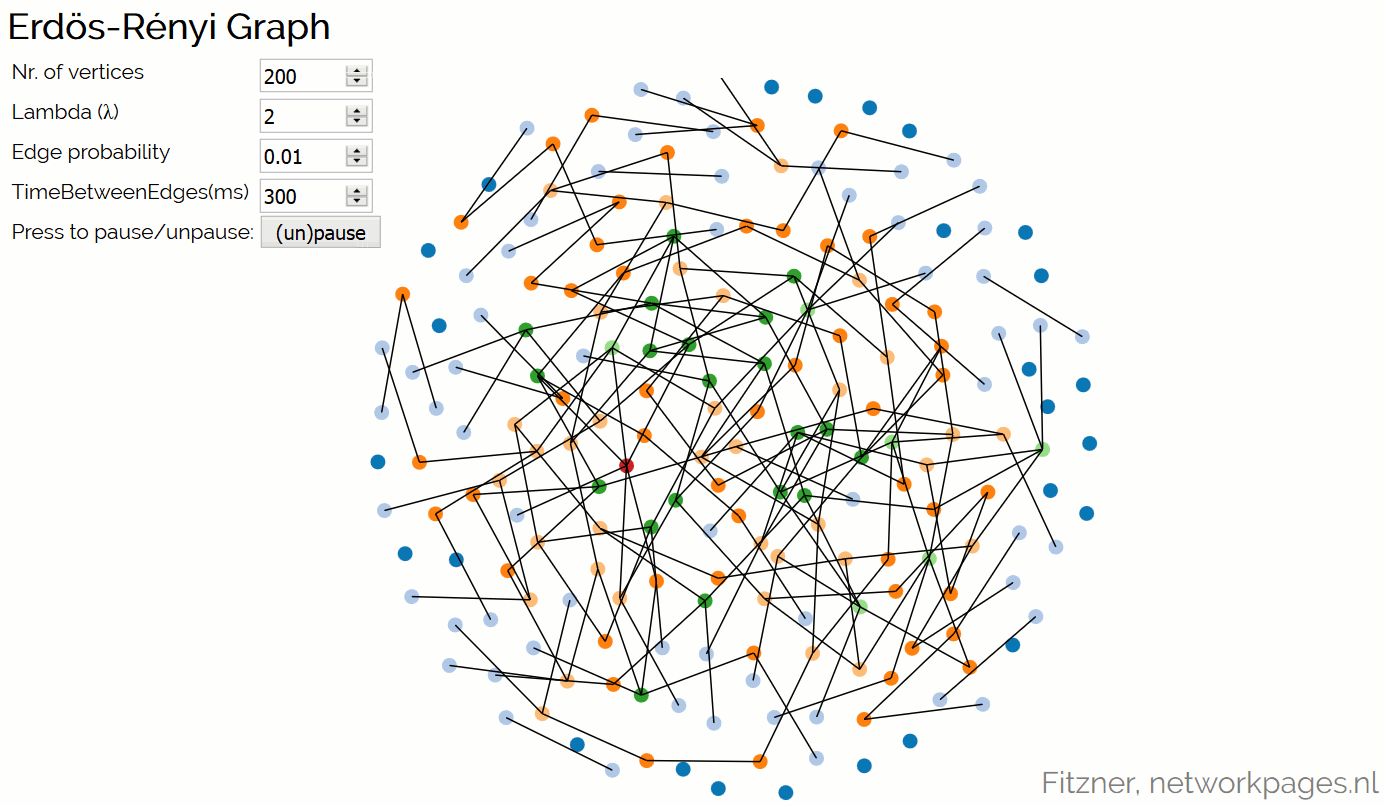
An animation that shows the creation of an Erdös-Rényi Graph. The parameters of the model are expected as input. Click on the picture to open the animation in full screen.
An animation that shows how a graph is created according to the configuration model. In this example the degrees are choose to uniformly from a interval. Click on the picture to open the animation in full screen.
This shows how the Dijkstra algorithm works.
This algorithm is used to compute the shortest way between location.
As example we use the streets of the Dutch town Brielle.
An explanation of the algorithm can be found here.
A simulation of an ideal gas, confined in a box with reflecting boundary.
You can download the program as an executable file as jar and as exe. To run the .jar file you will also need to have java on your system. The .exe file is able to run on windows systems that do not have java installed. Below you can find a small overview of the models that have been implemented.
Percolation on the two dimension lattice. You can observe the evolution of the system, by increasing the probability of keeping an edge step by step. A function to exports the simulation into pictures is integrated.
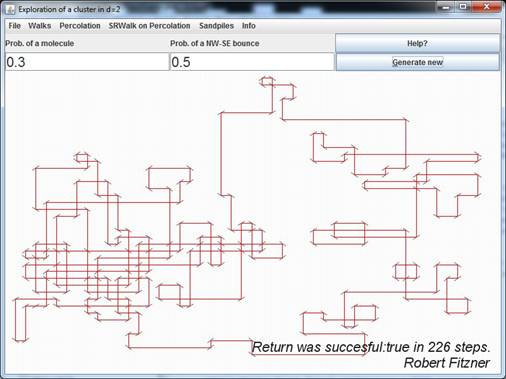
Implementation of a discrete Lattice gas model. This simulates the follow photons through a gas. Photons are flight through space and bounce of atoms/molecules. For mathematicians a major question is whether the photons will return to its original position.
- Bootstrap percolation,
- Invasion percolation,
- Frozen percolation,
- Random walk on percolation clusters,
- Exploration process of percolation cluster,
- The sandpile model in a two dimensional box,
- The sandpile model in an Erdös-Rényi Graph,
- Minesweeper (yes, really there is some very hard mathematics hidden in the game).