Research projects
I obtained my PhD in the field of statistical physics. Loosely speaking the idea of statistical physics is the following: We want to understand a complex system that influence by a huge number of factors. We replace complexity of the systems by randomness, which allows us to the mathematical tools for probability theory.
This makes some details no longer traceable, as they are replaced by random features. Most global features can however be easier analyzed/explained. This approach has been proven to be very successful in the last decades.
I was a research follow of the Institute for Complex Molecular Systems. This is a multidisciplinary research platform that enables the use of novel engineering tools and sophisticated modeling to stimulate research with a focus on chemistry and supramolecular chemistry. In several projects I assisted chemists in gaining understand of mechanism that are not directly observable.
It was a pleasure to be part of the academic world until 2019, when I had to leave the university for private reasons.
Below a small list of my former research projects.
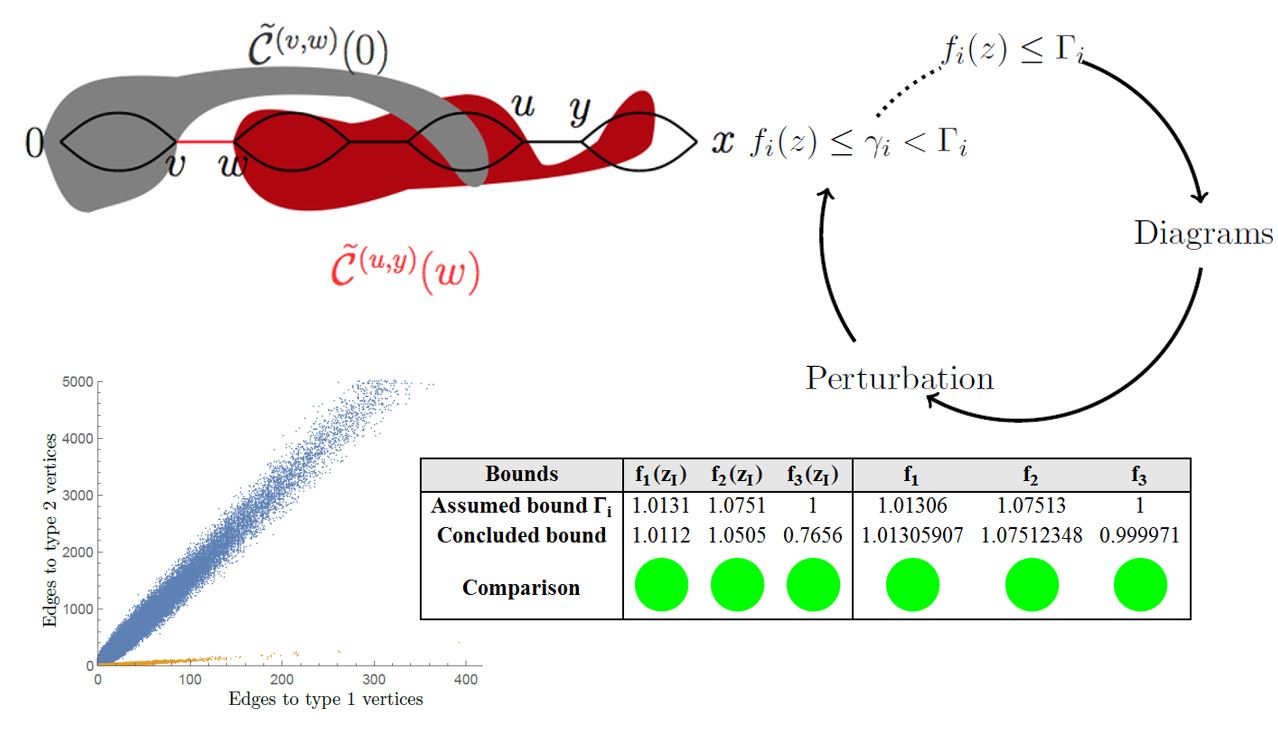
Remco van der Hofstad and I developed a mathematical technique to prove mean-field behavior
for several nearest-neighbor models in statistical physics.
It involves explicit computations for which dimensions
mean-field behavior can be proved rigorously for several nearest-neighbor systems.
A major goal of this project was to make the required analysis and computation as accessible as possible
for mathematician and theoretical physicists, which was previously not the case.
More information can be found here.

In a project with ICMS, we observed an ongoing chemical reaction in which individual molecules were imaged used a super-resolution microscope.
As the image were created using a super-resolution microscope only a small number of molecules are visible on each individual image.
The challenge was to deduce from the small number of visible localization the molecules the functioning of the process.
The result of this project were published in Science (2014).
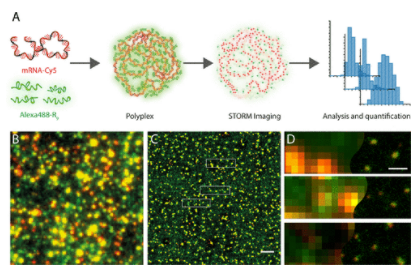
Building up on the earlier project, we used super-resolution imaging to study the structure and molecular composition of individual cell-penetrating peptides-mRNA polyplexes
with nanometer accuracy. These peptides are used to condense genetic material into nanoscale particles, called polyplexes, allowing to deliver mRNA into cells
in a safe and efficient way. We unveil the impact of peptide stoichiometry on polyplex structure and composition and to assess their destabilization in blood serum.
Our method provides information about the size and composition of individual polyplexes, allowing the study of such properties on a single polyplex basis.
The result of this project were published in Nano letters(2019).
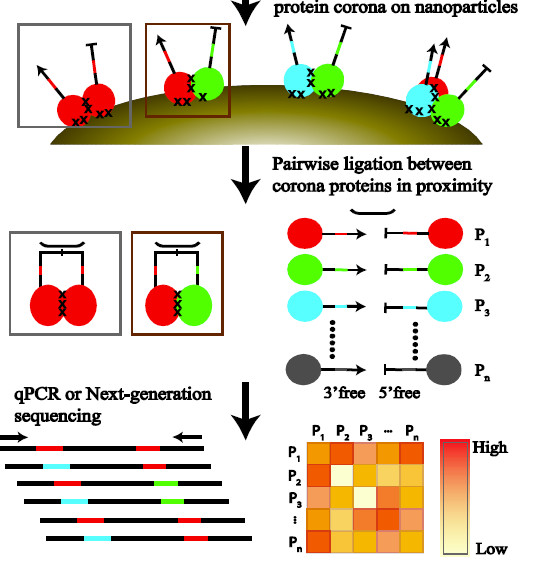
We want to understand the protein-protein interactions one the surface of nanoparticles. Such nanoparticles used in modern medicine with applications such as contrast agents and drug delivery systems. Nanoparticles in living organisms adsorb proteins on their surface. These proteins heavily influences the interaction between the particle and its surroundings. In this project we want to create a new methodology to measure the interaction between different kinds of proteins. The result of was finished in 2017, but has not been published in a journal up to this point.
In this project Maria Deijfen and I study the properties of random graphs consisting of nodes of two types.
These nodes create connections, in some random manner, which depend on the type of nodes involved.
We analyze the structure of the created random graph and derive explicite formulas for the number of edge
what are at least required to form one huge connected graphs.
More information can be found here.
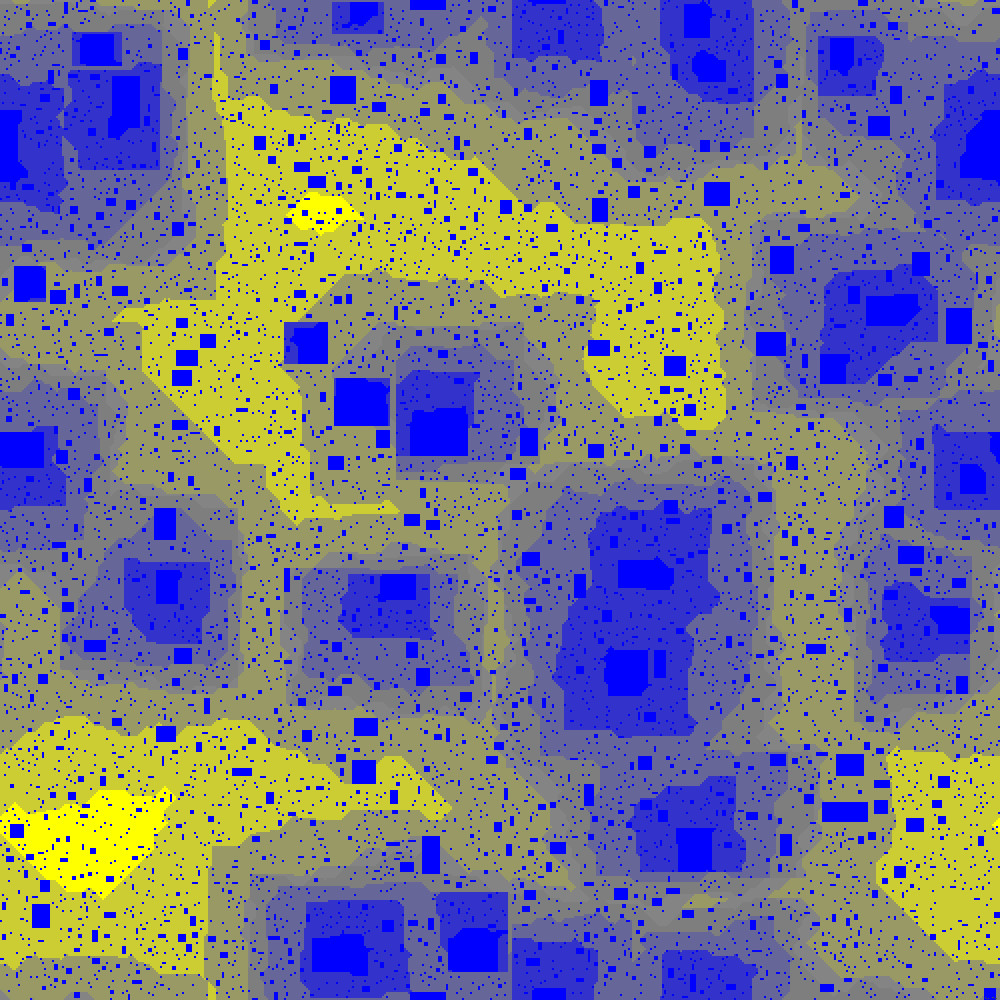
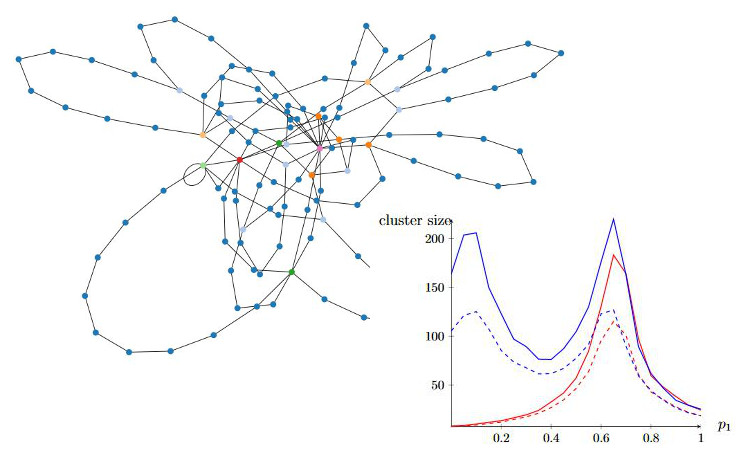
Tim Hulshof and I study a model called bootstrap percolation.
In this model a certain fraction of the populations is randomly infected.
The initial infected individuals, may then infect their neighbors in some non-random manner.
When the fraction of initial infected individuals is large enough everyone will be infected.
We perform a numerical study of the critical value of initial infected individuals
that are required to infected everyone.
In the corresponding picture the whole population was infected.
The color scale indicates at which time an individual was infected.
From dark blue for initial infected to yellow for being infected last.

The major subject of my study at the TU Berlin was in
mathematical finance. In this field mathematical models are used to compute the price of trading options.
This is usually done by deriving a trading strategy that replicates the value evolution of the trading options.
In my master thesis (Diplomarbeit) I consider a setting in which the usage of a general set of trading strategies
is either penalized (with a varying fee) or simply nor allowed, e.g. short-selling of options.
For this setting I derive the price for general trading options and described the construction of the corresponding trading strategies.